Здравствуйте, гость ( Вход | Регистрация )
 Объявление
Объявление
Проект Форума "Общие вопросы развития сознания" нацелен на содействие в поэтапном формировании активными участниками Проекта собственной мировоззренческой концепции, включающей в себя:
|
 23 May 2006, 08:15 23 May 2006, 08:15
Сообщение
#1
|
|
|
Администратор    Группа: Admin Сообщений: 2,083 Регистрация: 4.4.2005 Из: Санкт-Петербург Пользователь №: 32 Место жительства: Санкт-Петербург |
Зона первичных тезисов
Предлагаемая тема текущего обсуждения: Этап 2 : Сознание и эволюция Пространства Смысловые аспекты ---------------------------- Видеозаписи Семинаров II. Сознание и эволюция Пространства A_19_24.06.2006 Сознание и Эволюция пространства, структурные аспекты. A_20_26.08.2006 Сознание и Эволюция пространства, аспекты практики. A_21_07.10.2006 ОБЪЕКТИВНАЯ И СУБЪЕКТИВНАЯ РЕАЛЬНОСТЬ. . |
|
|
|
 |
Ответов
 3 Jul 2006, 23:34 3 Jul 2006, 23:34
Сообщение
#2
|
|
|
Активный участник    Группа: Участник Сообщений: 1,393 Регистрация: 7.3.2005 Из: Санкт-Петербург Пользователь №: 3 Место жительства: Санкт-Петербург |
Вариант подхода к рассмотрению Фрактальных Баз (ФБ) Постараемся максимально простым образом проявить структурные категории окружающего нас пространства, придерживаясь при этом структурных категорий выявленных в процессе предыдущего обсуждения. Учитывая фрактальность пространства, мы можем выбрать любую произвольную точку, приняв ее, условно, за некоторую нулевую точку нашего отсчета. Возьмем в качестве первичного объекта рассмотрения - произвольное точечное образование, не имеющее, с точки зрения выбранного нами уровня отсчета, никаких извнутренне проявленных тенденций и проявленных резонансных контуров, характеризующих его уровень сознательного проявления. Данный точечный объект будет изменять свое положение или характер состояния в рассматриваемом нами пространстве только в результате совокупности внешних воздействий, которые и будут реально определять характер его положения и состояния. Поэтому можно констатировать, что степень свободы действий данного объекта = 0, а уровень его стабилизации в окружающем пространстве будет также = 0. Совокупность подобных объектов выделим в отдельную категорию – называемую фрактальной базой (ФБ) и характеризующуюся нулевым уровнем самостабилизации и нулевой степенью свободы собственного самовыражения. Подобные объекты могут быть организованы или объединены в некую общность или множество только под воздействием каких-либо внешних воздействий, способным придать данным объектам некую внешнюю форму. Но как только внешняя форма потеряет степень своей выраженности или проявленности, так данные объекты, не имеющие никаких извнутренне проявленных тенденций к формированию внешних взаимодействий или взаимосвязей, распадутся на множество отдельных единиц, ничем не взаимосвязанных друг с другом. Теперь представим гипотетическую ситуацию, в которой данный объект совершая под действием внешнего воздействия последовательную смену своего положения и состояния вдруг теряет свою индифферентность к происходящим изменениям и пытается проявить некое стремление к целенаправленному выбору приемлемых с его точки зрения положений. Другими словами, допустим, что он проявит некую извнутренную направленность выбора своего положения или состояния. В этом случае можно будет говорить о некой векторности данного проявления. Но вектор представляет собой непрерывный бесконечный набор отдельных локально-точечных положений в рамках выделенного направления в окружающем нас пространстве. А это означает, что этот вектор не может быть образован из некоторого конечного числа отдельных точек. Подходя к этому вопросу с позиции математики мы можем записать выражение 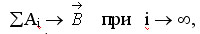 , ,(набор состояний точки А, отображенный как последовательность А и-тых, при бесконечном числе своих проявлений стремится к виду вектора В), т.е. при попытке объединения отдельных точечных образований в некую векторную единицу мы в пределе окажемся перед неким барьером, не имея принципиальной возможности реализовать данное стремление. Тем самым мы показали наличие принципиальной разницы между отдельной точечной позицией и понятием или категорией векторности. Теперь, по аналогии, перейдем к рассмотрению векторных категорий. Вектор имеет выраженную направленность своего проявления и возможность условно бесконечного разворота (роста) в выбранном направлении движения. Следовательно, данный объект характеризуется только одним извнутренне проявленным направленным стремлением или выбором, и в данном направлении может иметь бесконечно большую устойчивость проявления собственного стремления или самовыражения, т.е. можно сказать, что он имеет хотя бы один проявленный резонансный контур. По аналогии с предыдущим рассуждением мы можем констатировать наличие у векторного образования одной степени свободы и одного направления стабилизации. По другим направления наш вектор не имеет проявленных предпочтений или тенденций собственного самовыражения и, соответственно с этим, будет подвержен влиянию любых внешних воздействий, но с учетом взаимного соотношения абсолютных значений собственной векторности и внешнего воздействия. Совокупность подобных объектов выделим в отдельную категорию – называемую фрактальной базой (ФБ) и характеризующуюся первым уровнем самостабилизации и одной степенью свободы собственного самовыражения. Теперь попытаемся представить себе, что по каким-то неизвестным нам причинам у данного объекта зародилось сомнение в правильности выбранного направления, и он попытался внести коррективы в направление своего выраженного стремления, т.е. проявил направленность, не совпадающую с ранее им проявленной. В этом случае он «охватит» своим устремлением некоторое плоскостное образование. Теперь, мы будем вынуждены признать невозможность сведения этого небольшого фрагмента плоскости, заключенного между двух векторов к сумме некоторого наперед заданного числа аналогичных векторных образований ввиду наличия очередного предельного перехода, т.к. всегда между двумя соседними в нашем рассмотрении векторами всегда можно будет разместить еще как минимум один вектор. А это опять означает, что пытаясь набрать некоторую плоскость из отдельных векторных единиц мы можем сколь угодно близко приближаться к целостному плоскостному образованию, но никогда не сможем его реально получить. Это означает, что мы проявили еще одну принципиальную границу, отделяющую линейные категории от плоскостных. Совокупность рассмотренных объектов, обладающих поверхностью, содержащей в себе бесконечное число векторных образований, способных одновременно проявить два взаимоортогональных направления собственного развития или стабилизации в окружающем их пространстве отнесем к фрактальной базе, содержащей объекты с двумя степенями свободы и двумя направлениями одновременной самостабилизации и самовыражения. Интерполируя ранее приведенные рассуждения на зону перехода от плоскостных категорий к трехмерным мы получим аналогичную ситуацию – пространственные образования будут структурно отделены от плоскостных некоторым барьерным уровнем, не позволяющим осуществить переход из одной категории в другую путем простого количественного увеличения уже имеющихся характеристик или потенциала. Итак, на данном этапе нашего рассмотрения выделены уже 4 принципиально отличные структурные категории пространственных состояний. Самым интересным в нашем теперешнем рассмотрении будет то, что переход от 3-х мерного образования к 4, 5, 6 и т.д. мерным образованиям не будет содержать ранее рассмотренных барьерных уровней. Т.е., начиная с цифры 3 процесс увеличения мерности рассмотрения будет являться не вариантом качественного изменения состояния объекта, а количественным параметром. Но, попытавшись продолжить наше рассмотрение подобным образом, мы опять наталкиваемся на очередной принципиальный барьер – а именно, увеличивая мерность рассматриваемых нами пространственных категорий мы никогда не сможем достичь бесконечной мерности этого рассмотрения. А это означает наличие еще одного предельного перехода отделяющего одну фрактальную базу от другой. В данном случае речь идет об объектах, хараетризующихся мерностью пространственной стабилизации и самовыражения от 3 до Ґ. Возникает вопрос, а возможно ли принципиально сформировать систему взаимосвязей, изначально имеющую бесконечное число равнозначных взаимно ортогональных направлений стабилизации и соответственное же число степеней свободы своего извнутреннего самовыражения? Да, действительно, ответ напрашивается сам собой – реализация данного положения становиться возможным, если в качестве рабочей модели будет взята сфера, имеющая всего два параметра своего определения в виде координаты центра и радиуса сферы при абсолютной однозначности определения координат любой точки на своей поверхности. Теперь осталось свести результаты нашего рассмотрения в таблицу и завершить текущий анализ рядом сопутствующих заключений. |
|
|
|
Сообщений в этой теме
 Администратор II. Сознание и эволюция Пространства 23 May 2006, 08:15
Администратор II. Сознание и эволюция Пространства 23 May 2006, 08:15
 Игорь Журкин Предлагаемая тема пугает своей глобальностью. На м... 24 May 2006, 20:26
Игорь Журкин Предлагаемая тема пугает своей глобальностью. На м... 24 May 2006, 20:26
 Наташа Егорова В дополнение к вышесказанному разбиению на направл... 25 May 2006, 00:06
Наташа Егорова В дополнение к вышесказанному разбиению на направл... 25 May 2006, 00:06
 Зыгарь Татьяна Предлагаю к рассморению компактную формулировку Пр... 30 May 2006, 17:01
Зыгарь Татьяна Предлагаю к рассморению компактную формулировку Пр... 30 May 2006, 17:01
 --- Мне кажется, что при рассмотрении предложенной тем... 31 May 2006, 09:32
--- Мне кажется, что при рассмотрении предложенной тем... 31 May 2006, 09:32
 Александр Алексейцев .......... Итак, для успешного анализ... 7 Jun 2006, 20:17
Александр Алексейцев .......... Итак, для успешного анализ... 7 Jun 2006, 20:17
 --- Цитата(Александр Алексейцев @ 7 Jun 2006, 23... 8 Jun 2006, 17:42
--- Цитата(Александр Алексейцев @ 7 Jun 2006, 23... 8 Jun 2006, 17:42
 Наташа Егорова Я думаю, мы забуксовали с рассмотрением данного во... 8 Jun 2006, 20:19
Наташа Егорова Я думаю, мы забуксовали с рассмотрением данного во... 8 Jun 2006, 20:19
 --- Мне кажется, что нужный на данном этапе Проекта те... 10 Jun 2006, 10:36
--- Мне кажется, что нужный на данном этапе Проекта те... 10 Jun 2006, 10:36
 Elhfi Если рассматривать пространство как эволюционную, ... 10 Jun 2006, 19:21
Elhfi Если рассматривать пространство как эволюционную, ... 10 Jun 2006, 19:21

 Игорь Журкин Цитата(Elhfi @ 10 Jun 2006, 20:21) Простр... 24 Jun 2006, 17:21
Игорь Журкин Цитата(Elhfi @ 10 Jun 2006, 20:21) Простр... 24 Jun 2006, 17:21

 Elhfi Цитатаэто элемент Пространства, состояние которого... 30 Jun 2006, 11:24
Elhfi Цитатаэто элемент Пространства, состояние которого... 30 Jun 2006, 11:24
 --- Цитата(Elhfi @ 10 Jun 2006, 22:21) Таким ... 12 Jun 2006, 12:47
--- Цитата(Elhfi @ 10 Jun 2006, 22:21) Таким ... 12 Jun 2006, 12:47
 Администратор Итак, последние рассуждения неизбежно привели к в... 12 Jun 2006, 14:58
Администратор Итак, последние рассуждения неизбежно привели к в... 12 Jun 2006, 14:58
 Александр Алексейцев Вариант первичного рассмотрения.
Пространство - э... 12 Jun 2006, 20:58
Александр Алексейцев Вариант первичного рассмотрения.
Пространство - э... 12 Jun 2006, 20:58
 Галина Бельская Для меня такие понятия, как сознание и пространств... 12 Jun 2006, 21:12
Галина Бельская Для меня такие понятия, как сознание и пространств... 12 Jun 2006, 21:12
 Наташа Егорова Пространство "происходит" в результате разворота т... 15 Jun 2006, 20:26
Наташа Егорова Пространство "происходит" в результате разворота т... 15 Jun 2006, 20:26
 --- ЦитатаИтак, развертывание биологического организма... 17 Jun 2006, 10:37
--- ЦитатаИтак, развертывание биологического организма... 17 Jun 2006, 10:37
 Игорь Журкин Цитата(Сергей Лептуга @ 17 Jun 2006, 11:3... 18 Jun 2006, 17:45
Игорь Журкин Цитата(Сергей Лептуга @ 17 Jun 2006, 11:3... 18 Jun 2006, 17:45
 Elhfi Если применять центрическую модель в отношении пон... 18 Jun 2006, 22:11
Elhfi Если применять центрическую модель в отношении пон... 18 Jun 2006, 22:11

 Наташа Егорова Цитата(Elhfi @ 18 Jun 2006, 23:11) Если п... 25 Jun 2006, 23:24
Наташа Егорова Цитата(Elhfi @ 18 Jun 2006, 23:11) Если п... 25 Jun 2006, 23:24

 Elhfi ЦитатаЗдесь нужно соблюсти золотую середину, постр... 1 Jul 2006, 12:59
Elhfi ЦитатаЗдесь нужно соблюсти золотую середину, постр... 1 Jul 2006, 12:59
 Администратор О ТЕКУЩЕМ МОМЕНТЕ
В процессе текущего обсужд... 20 Jun 2006, 22:44
Администратор О ТЕКУЩЕМ МОМЕНТЕ
В процессе текущего обсужд... 20 Jun 2006, 22:44

 Игорь Журкин Цитата(Администратор @ 20 Jun 2006, 23:44... 20 Jun 2006, 23:08
Игорь Журкин Цитата(Администратор @ 20 Jun 2006, 23:44... 20 Jun 2006, 23:08

 --- Цитата(Игорь Журкин @ 21 Jun 2006, 02:08)... 21 Jun 2006, 06:30
--- Цитата(Игорь Журкин @ 21 Jun 2006, 02:08)... 21 Jun 2006, 06:30
 Игорь Журкин Но ведь никто не запрещает обозначать и эти самост... 21 Jun 2006, 10:21
Игорь Журкин Но ведь никто не запрещает обозначать и эти самост... 21 Jun 2006, 10:21
 Игорь Журкин Просили резюме по последнему вопросу.
…... 22 Jun 2006, 15:14
Игорь Журкин Просили резюме по последнему вопросу.
…... 22 Jun 2006, 15:14
 Игорь Журкин Цитата(Elhfi @ 18 Jun 2006, 23:11) Важным... 24 Jun 2006, 17:41
Игорь Журкин Цитата(Elhfi @ 18 Jun 2006, 23:11) Важным... 24 Jun 2006, 17:41
 Администратор Итак, завершился первый этап обсуждения фундамента... 28 Jun 2006, 00:04
Администратор Итак, завершился первый этап обсуждения фундамента... 28 Jun 2006, 00:04
 Татьяна Алексейцева Развитие сознания.
До сих пор рассмотрение вопрос... 30 Jun 2006, 12:28
Татьяна Алексейцева Развитие сознания.
До сих пор рассмотрение вопрос... 30 Jun 2006, 12:28
 --- Наверное, можно использовать простой способ диффер... 3 Jul 2006, 14:37
--- Наверное, можно использовать простой способ диффер... 3 Jul 2006, 14:37
 Галина Бельская Фрагмент заметок, созвучный с темой текущего обсуж... 24 Jul 2006, 10:36
Галина Бельская Фрагмент заметок, созвучный с темой текущего обсуж... 24 Jul 2006, 10:36
 Игорь Журкин В настоящий момент возникла ситуация, когда отс... 14 Aug 2006, 12:16
Игорь Журкин В настоящий момент возникла ситуация, когда отс... 14 Aug 2006, 12:16
 Игорь Журкин Вся эта куча текста, представляющего собой линейны... 14 Aug 2006, 15:57
Игорь Журкин Вся эта куча текста, представляющего собой линейны... 14 Aug 2006, 15:57
 Игорь Журкин Итак, мы кратко изложили
некоторые подходы к п... 14 Aug 2006, 15:59
Игорь Журкин Итак, мы кратко изложили
некоторые подходы к п... 14 Aug 2006, 15:59
 Администратор ЗОНА ТЕКУЩЕГО ОБСУЖДЕНИЯ
Тема: Сознание и эволюци... 30 Aug 2006, 17:26
Администратор ЗОНА ТЕКУЩЕГО ОБСУЖДЕНИЯ
Тема: Сознание и эволюци... 30 Aug 2006, 17:26
 --- ЦитатаЧеловек, достигающий состояния «стволовой кл... 6 Sep 2006, 14:21
--- ЦитатаЧеловек, достигающий состояния «стволовой кл... 6 Sep 2006, 14:21
 Татьяна Алексейцева ЦитатаНеобходимо подчеркнуть, что Сознание являетс... 2 Oct 2006, 15:10
Татьяна Алексейцева ЦитатаНеобходимо подчеркнуть, что Сознание являетс... 2 Oct 2006, 15:10
 Александр Алексейцев Что можно сопоставить с понятием практических аспе... 6 Oct 2006, 22:11
Александр Алексейцев Что можно сопоставить с понятием практических аспе... 6 Oct 2006, 22:11
 Татьяна Алексейцева Проблемы, связанные с практической реализацией люб... 12 Oct 2006, 15:20
Татьяна Алексейцева Проблемы, связанные с практической реализацией люб... 12 Oct 2006, 15:20
 Татьяна Алексейцева Необходимо учитывать, что фрактальный разворот гип... 17 Oct 2006, 15:52
Татьяна Алексейцева Необходимо учитывать, что фрактальный разворот гип... 17 Oct 2006, 15:52
 Александр Алексейцев Объективная и субъективная реальность
Когда мы г... 17 Oct 2006, 21:52
Александр Алексейцев Объективная и субъективная реальность
Когда мы г... 17 Oct 2006, 21:52
 Александр Алексейцев ОБЪЕКТИВНАЯ И СУБЪЕКТИВНАЯ РЕАЛЬНОСТЬ.
Ранее бы... 17 Oct 2006, 21:59
Александр Алексейцев ОБЪЕКТИВНАЯ И СУБЪЕКТИВНАЯ РЕАЛЬНОСТЬ.
Ранее бы... 17 Oct 2006, 21:59
 Татьяна Алексейцева Как достичь объективного суждения по интересующему... 20 Oct 2006, 09:02
Татьяна Алексейцева Как достичь объективного суждения по интересующему... 20 Oct 2006, 09:02
 Наташа Егорова Реализация происходит как адаптация осознанных кат... 1 Nov 2006, 23:56
Наташа Егорова Реализация происходит как адаптация осознанных кат... 1 Nov 2006, 23:56
 Александр Алексейцев Аспекты реализации 13 Nov 2006, 10:24
Александр Алексейцев Аспекты реализации 13 Nov 2006, 10:24
 --- Думаю, что возможность говорить об аспектах реализ... 18 Nov 2006, 11:21
--- Думаю, что возможность говорить об аспектах реализ... 18 Nov 2006, 11:21
 Татьяна Алексейцева Вариант Резюме по теме.
Развитие сознания и прос... 22 Nov 2006, 23:27
Татьяна Алексейцева Вариант Резюме по теме.
Развитие сознания и прос... 22 Nov 2006, 23:27
 Игорь Журкин Итак, опираясь уже на изложенные
ранее тезисы,... 23 Nov 2006, 23:22
Игорь Журкин Итак, опираясь уже на изложенные
ранее тезисы,... 23 Nov 2006, 23:22
 Elhfi Каждая система , представляющая собой фрактал или ... 15 Dec 2006, 20:46
Elhfi Каждая система , представляющая собой фрактал или ... 15 Dec 2006, 20:46
 --- Вариант резюме по теме.
Структурные аспекты Прост... 18 Dec 2006, 15:53
--- Вариант резюме по теме.
Структурные аспекты Прост... 18 Dec 2006, 15:53  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0
| Текстовая версия | Сейчас: 12th July 2025 - 09:18 |
Русская версия IP.Board
2.3.1 © 2025 IPS, Inc.
Лицензия зарегистрирована на: Форум "Общие вопросы развития сознания"